Forced convection constant is a non-linear function of the fan speed
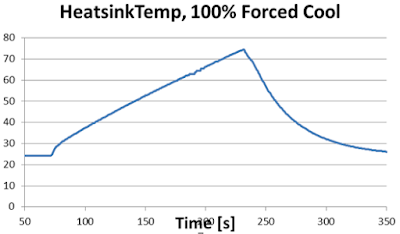
Regardless of whether forced or unforced, all heatsinks have thermal mass (capacitance). So an easy way to think about the problem at a high level is to consider the change in the thermal resistance from the heatsink fins to the ambient (air if air cooled, or liquid if liquid cooled). If I plot Tsink - Tambient (the temperature of the heatsink relative to the ambient) with DC fan at max speed, I may see a classical RC circuit cooling behavior, like this:
Heatsink convection vs. air speed
A simplified model of convection is Q = h (Tsink - Tambient), and the problem boils down to estimating the convection constant for various conditions. I remember the scary integrals in the heat transfer class, which are often done in FEA these days. I didn't do well in fluid mechanics or heat transfer, but was able to follow along a heat transfer textbook: Engineering Heat Transfer 2nd Edition, by Rathore and Kapuno. On page 563, there is a heatsink fan configuration that looks similar to mine (array of cylinderical rods facing the air), so I started there. For forced air convection, the h term is Nu ∙ kf / D, where
- kf is the thermal conduction coefficient of air film around heat fin. Typically, we would just look up the value at an average temperature of (Tsink + Tambient)/2. Between 26.3 ~ 30E-3 W/m∙K for 300~350 K.
- D is the rod diameter, say 2 mm.
- Nu is the Nusselt number that depends on Reynolds number (which in turn depends on the forced air speed). For my configuration, the textbook says it is 0.27 ∙ (u_air D / ν)^0.63 ∙ Pr^0.36 ∙ (Pr∞ / Prsink)^1/4, where
- u_air is the bluk air speed through the heatsink,
- ν is the air viscosity, ranging 15.89 to 20.92 m2/s for air between 300 to 350 K,
- Pr is the Prandtl number: 0.707 at 300 K and 0.700 at 350 K.
- The Nu therefore works out to something like 0.7E-3 u_air^0.63
Note that Nu depends the most on the air speed uair, namely, non-linearly as a power of 0.63. With this Nu, you are supposed to solve for the temperature of the air leaving the heatsink fins: Texit = Tsink – (Tsink – Tambient) exp[-π D N h / (ρ u_air N_T p_T C_p)], where:
- N is the total number of fins
- h was calculated above,
- N_T is the number of rods in the transverse plane
- ρ is air density, about 1 Kg/m3 around 300~350 K
- p_T is the fin spacing (pitch)
- C_p is the air's heat capacity (about 1 J/g∙K)
After substitution, you arrive at Texit = Tsink – (Tsink – Tambient) exp[Ca / u_air0.37], where C_a is depends on your situation. What this equation says is that the exit temperature at the heatsink is almost the Tambient at all air speeds except the really slow case, in which case the exit temperature is almost the Tsink, driven by this example of the exponential term:
Intuitively, convection from a heatsink is NOT from Tsink, but rather a temperature that is closer to Tambient. How close depends on the heatsink shape and air speed.
Finally, what you really want to know is the aggregate heat flow from the heatsink to the ambient air. For the N number of rod case, Qconvect = N (h π D L) ∆T = π N ∙ Nu ∙ kf ∙ L ∙ ∆T, where:
- ∆T is calculated above--practically speaking something like 90% of (Tsink - Tambient),
- L is the rod height
Since Nu is proportional to (u_air D / ν)^0.63, Qconvect ~ some_number ∙ u_air^0.63 ∙ (Tsink – Tambient) for all but the very low air speeds.
Now that you understand, keep the simplest 1 equation
If the textbook was completely applicable for my case, I should be able to predict the 1/RC slope for all forced air cooling based on the airspeed--which according to the DC fan manufacturer scales linearly with the fan speed. But instead of u_air^0.63, I found a factor of u_air^0.8 to be a better fit. So instead of losing sleep over the discrepancy, I will just use the power of 1/0.8 = 1.25 when calculating the desired fan speed. That is, my forced air heatsink is simply characterized by
Qconvect(duty) = [h@100% * duty^0.8 + h@0%] (Tsink - Tambient),
where 0 <= duty <= 1 ; that is, consisting of the forced and natural convection terms.
Custom Simscape component for the forced air heatsink
I explained the steps to creating a custom Simscape component in a previous blog. Here is the Simscape code for the above heat flux equation:
component Heatsink
% Heatsink: 2
% If the duty cycle is s, where 0 <= s <= 1,
% q = Csink (h100 * s^0.8 + h0) (H - C)
%
% where the following parameters are treated as constants for this simple
% model:
%
% * h100: convection constant at max fan duty cycle [W/K]
%
% * h0: natural convection constant [W/K]
nodes %conserving ports
H = foundation.thermal.thermal; % H:top
C = foundation.thermal.thermal; % C:bottom
end
parameters
h100 = {0.032, 'W/K'};
h0 = {0.0019, 'W/K'};
end
inputs
s = {0, '1'};% s:bottom
end
variables(Access=private)
q = { 0, 'W' }; % heat flux
end
function setup
if h0 <= 0
pm_error('simscape:GreaterThanZero', 'h0')
end
if h100 < 0
pm_error('simscape:GreaterThanZero', 'h100')
end
end
branches % Relationship between the Through variables
q : H.Q -> C.Q;%In heatsink, heat flows hot to cold
end
equations % Relationship between the Across variables
q == (h100 * s^0.8 + h0) * (H.T - C.T);
end % equation
end %component
And while I may yet get tired of such frivolities, I got a picture of a heatsink from Bing Images and put it right next to the source code during the compilation of my simscape library, so that this custom component may show up as a picture.
Simulate cooling a hot block with the heatsink
As a sanity test, set the initial temperature of the heatsink at 100 C, when turn the fan on at 50% duty cycle. Here is the Simscape block diagram for it:
And here is the 10000 second simulation result:
As you can see, this heatsink is not all that powerful.
